この記事にはプロモーションが含まれています。
アフィン変換の学習のために、opencvなどのライブラリを使わずにアフィン変換をかけるコードを作成しました。
アフィン変換 : 線形変換 + ユークリッド変換
アフィン変換とは、画像に対して拡大・縮小、回転、せん断、並進の画像処理をかける処理で、線形変換とユークリッド変換を含む変換になります。
行列において、拡大・縮小、回転、せん断の変換は原点座標を中心に変換がかけられます。画像に対しては、並進処理もかけるのが一般的なので、アフィン変換行列は3×3行列で表現されます。
変換前の座標を\((x, y)\)、変換後を\((x’, y’)\)とすると、以下のように記述されます。
$$ \begin{bmatrix}x’ \\ y’ \\1 \end{bmatrix} = \begin{bmatrix}a & b & c \\d & e & f\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}x \\ y \\1 \end{bmatrix} $$
ライブラリを使わない実行コード例
まずは、作成したコードを実行したときの様子の動画はこちらになります。
実行コードはこちら。
import cv2
import numpy as np
# 入力画像の読み込み
image = cv2.imread('input_image.bmp')
image = cv2.resize(image, dsize=None, fx=2, fy=2, interpolation=cv2.INTER_LANCZOS4)
print(image.shape)
# 入力画像のサイズを取得
height, width = image.shape[:2]
# アフィン変換行列を作成(例: 回転)
angle = 45 # deg
angle = angle / 180 * np.pi
affine_matrix = np.float32([[np.cos(angle), -np.sin(angle), 0],
[np.sin(angle), np.cos(angle), 0],
[0, 0, 1]])
## グリッドラインに対するアフィン変換
# 基底のグリッドラインを作成
grid_size = 50 # グリッドのセルのサイズ
grid_color = (0, 0, 255) # グリッドの色 (BGR形式)
grid_thickness = 2 # グリッドの線の太さ
grid_image = np.zeros_like(image)
for y in range(0, height, grid_size):
cv2.line(grid_image, (0, y), (width-1, y), grid_color, grid_thickness)
for x in range(0, width, grid_size):
cv2.line(grid_image, (x, 0), (x, height-1), grid_color, grid_thickness)
# ピクセルごとのアフィン変換と可視化
transformed_grid_image = np.zeros_like(grid_image)
for y in range(height):
for x in range(width):
point = np.array([x, y, 1])
transformed_point = np.dot(affine_matrix, point)
transformed_x, transformed_y, _ = transformed_point.astype(int)
# 変換後の座標が画像範囲内の場合のみピクセル値をコピー
if 0 <= transformed_x < width and 0 <= transformed_y < height:
transformed_grid_image[transformed_y, transformed_x] = grid_image[y, x]
# グリッドラインの可視化
cv2.imshow('Input Grid', grid_image)
cv2.imshow('Transformed Grid', transformed_grid_image)
## 入力画像に対するアフィン変換
# 出力画像の配列を作成
output_image = np.zeros_like(image)
# ピクセルごとのアフィン変換と可視化
i=0
for y in range(height):
for x in range(width):
point = np.array([x, y, 1])
transformed_point = np.dot(affine_matrix, point)
transformed_x, transformed_y, _ = transformed_point.astype(int)
# 変換後の座標が画像範囲内の場合のみピクセル値をコピー
if 0 <= transformed_x < width and 0 <= transformed_y < height:
output_image[transformed_y, transformed_x] = image[y, x]
# 入力画像と出力画像の表示
if i % 100 == 0:
cv2.imshow('Input Image', image)
cv2.imshow('Output Image', output_image)
cv2.waitKey(1) # 1ミリ秒の待機(可視化のためのウェイト)
i= i+1
outfilename = "affine"
cv2.imwrite(outfilename + "_00_grid.jpg", grid_image)
cv2.imwrite(outfilename + "_01_affine-grid.jpg", transformed_grid_image)
cv2.imwrite(outfilename + "_10_inimg.jpg", image)
cv2.imwrite(outfilename + "_11_affine-inimg.jpg", output_image)
cv2.destroyAllWindows()アフィン変換前の座標(x, y)の画素がアフィン変換Aにより、座標(x’, y’)に移動します。行列で記載すると、
$$ \bf x’=Ax $$
となるので、これを素直に適用します。コードでは以下の箇所になります。
point = np.array([x, y, 1])
transformed_point = np.dot(affine_matrix, point)また、こちらのコードでは、グリッド線に対して、アフィン変換をかけた結果が確認できます。OpenCVの仕様上、原点座標が画像左上になっていることを注意してください。(いわゆるuv座標系)
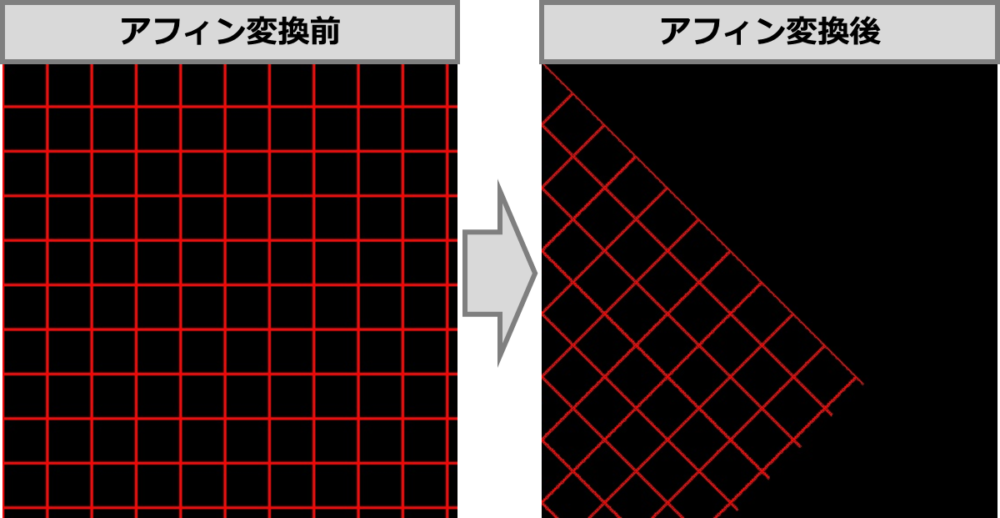
アフィン変換は線形変換なため、別のアフィン変換と線形結合可能です。
例えば、鏡映後に並進をかける場合は、それぞれのアフィン行列の内積をとった行列を作用させるようにしましょう。
# 鏡映
affine_matrix_reflct = np.float32([[-1, 0, 0],
[0, 1, 0],
[0, 0, 1]])
# 並進
tx = 512
ty = 0
affine_matrix_tran = np.float32([[1, 0, tx],
[0, 1, ty],
[0, 0, 1]])
affine_matrix = np.dot(affine_matrix_tran, affine_matrix_reflct)このコードはライブラリに頼っていないため、アフィン変換後の座標の値に歯抜けの画素が出てくる可能性があります。実際、45度の回転のアフィン変換をかけた画像を拡大すると、ところどころドット抜けがあります。

opencvなどのライブラリで実装した場合、歯抜け画素に対しての補間処理がかけられるので、きれいな画像に仕上がります。



コメント